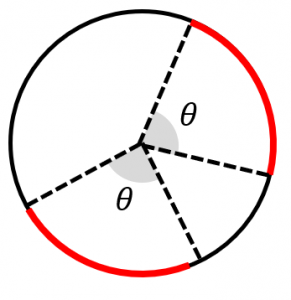
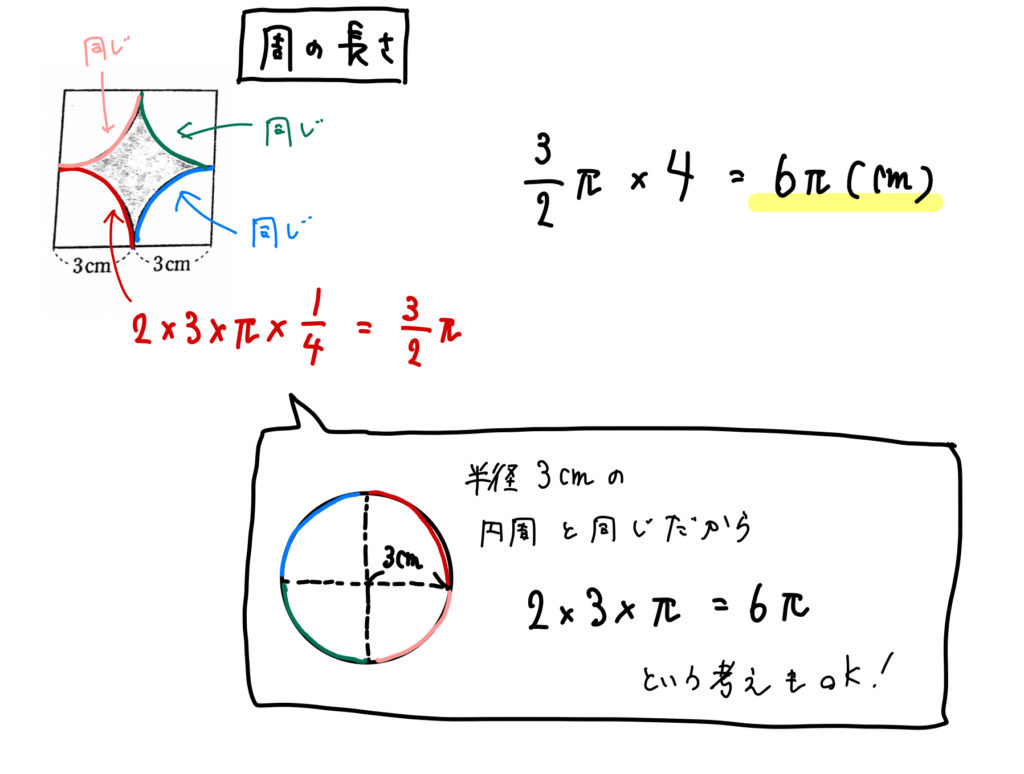
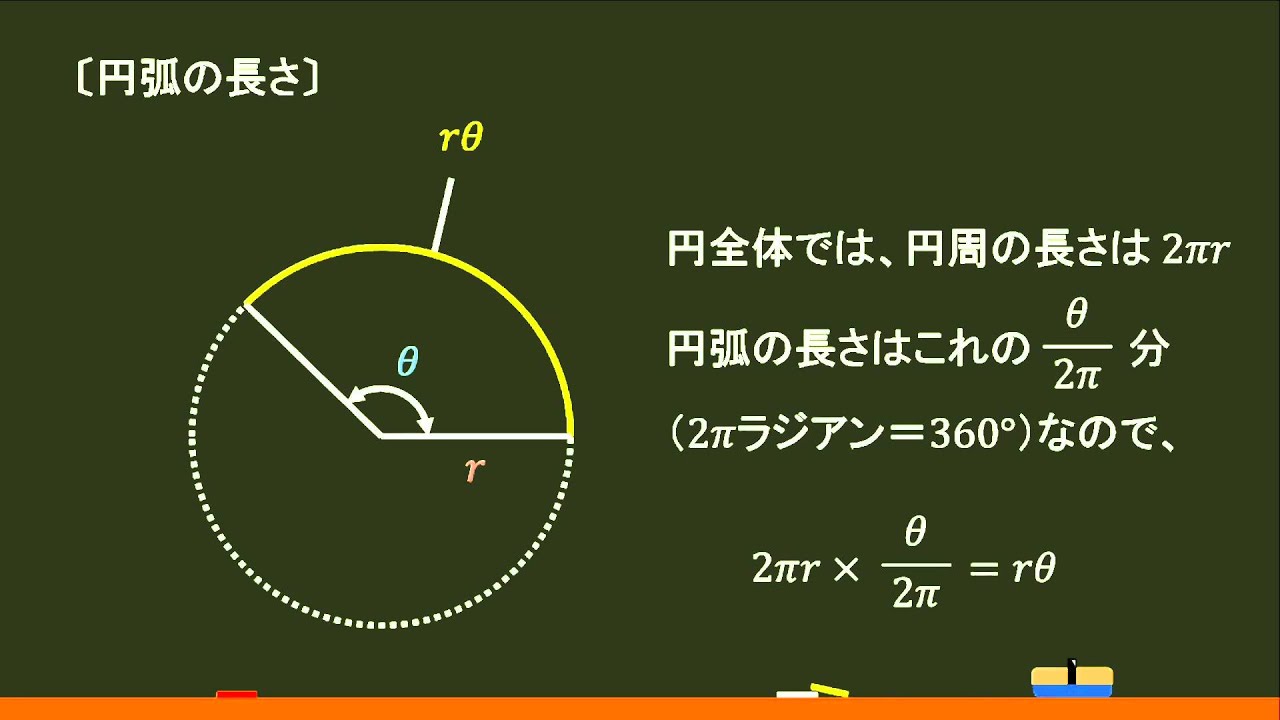
弧の長さ は、 r θ と表されるので、中心角に比例します。 一方、 弦の長さ は、 2 r sin θ 2 と表されるので、中心角には比例しません。 また、中心角が等しい場合、 弧の長さ は 弦の長さ よりも長いです。 どちらも、 0 ∘ ≤ θ ≤ 180 ∘ の範囲では扇形の中心角は弧の長さに比例するので、中心角 x° とすると x = 360× 弧の長さ 円周の長さ = 360× 4π 2π × 3 = 240 x = 360 × 弧 の 長 さ 円 周 の 長 さ = 360 × 4 π 2 π × 3 = 240 したがって、中心角は 240° と求まりました。 あとは、一般的な扇形の面積を求める公式を使って S = πr2 × x 360∘ = π ×32 × 240 360 = 6π S = π r 2 × x 360 ∘ = π × 3 2 × 240 360 = 6 π となります。 他の平面図形の正方形の周りの長さの求め方は「一辺の長さ×4」です。 例えば、一辺の長さが5cmの正方形の周りの長さ=5cm×4=cmです。 逆に、正方形の周りの長さが分かっていれば「4で割る」ことで、一辺の長さを算定できます。 また、長方形の周りの長さ= (縦の長さ横の長さ)×2です。 今回は、正方形の周りの長さの求め方、長方形の周りの長さについて説明します

扇形の弧の長さの求め方 公式と計算例
扇形の周りの長さの求め方
扇形の周りの長さの求め方- 扇形の周りの長さが18、面積が18、扇形の中心角を求めなさいという問題を解ける方教えて欲しいです。解説まで入れてくださると助かります。扇形の半径を r、中心角を θ° と置くと、2r 2πr(θ/360) = 18, 1π(r^2)(θ/360) = 18 なので、 円周の長さ = 直径 × 円周率 となります。 おうぎ形の弧の長さ 円周の長さのうち 扇形は「円の 分の1」になっているかが重要です。 扇形の部分が円の「何分の1」なのかがわかれば簡単に解くことができます。




おうぎ形の弧長 面積 中心角 半径 具体例で学ぶ数学
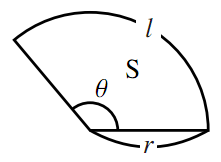
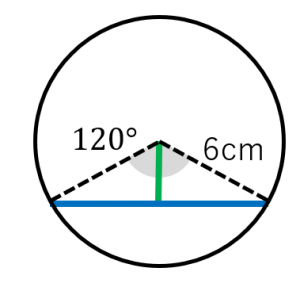
半円の周りの長さや、円や図形を組み合わせた問題などが出題されます。 簡単な問題が出来るようになったら、中学入試レベルの応用問題も取り組んでみてください。 ポイント 半円の周り長さは直径の部分も忘れずに求めましょう。 半円の周りの長さ 「扇形の弧の長さ」と「扇形の面積」の公式を用いれば中心角を削除することができます。 『 S= 1 2lr S = 1 2 l r 』というように面積を半径と弧の長さから求めることができるのです。 上記の例題の場合、 S=1 2 ×10π ×6 = 30π S = 1 2 × 10 π × 6 = 30 π 答えは 30πcm2 30 π c m 2 です。 『 S= 1 2lr S = 1 2 l r 』は一応は公式として習いますが、あまり頻繁に使うものでもないです "扇形の弧の長さと面積"の公式とその証明です! 扇形の弧の長さと面積公式扇形の弧の長さと面積半径r、中心角θ、弧の長さl、面積Sとすると \(・l=rθ\) \(・S=\frac{1}{2}r^2θ=\frac{1}{2}lr\)証明
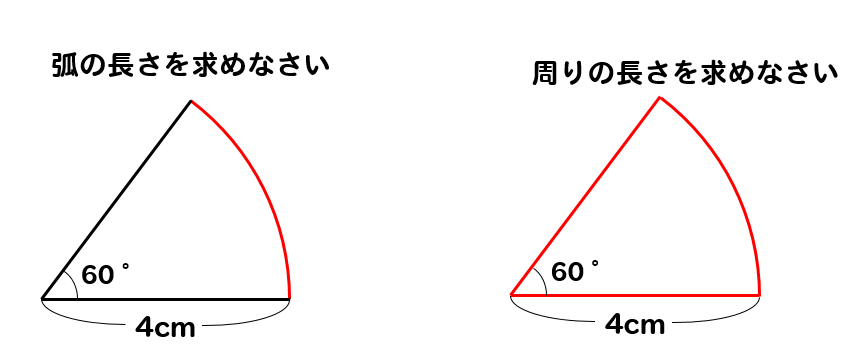
おうぎ形(扇形)の半径と中心角を入力すると、その面積、弧の長さ、周囲の長さ、弦の長さが出力されます。中心角は 0 〜 360 までの値を入れてください。度(°)の記号は不要です。数字は半角のみ。周りの長さとは、弧の長さと半径を2個分合わせた長さのことでしたね。 まずは弧の長さを求めてみましょう。 弧の長さの公式に当てはめてみると $$2\pi\times4\times\frac{60}{360}$$ $$=8\pi\times\frac{1}{6}$$ $$=\frac{4}{3}\pi$$ 弧の長さは\(\frac{4}{3}\pi\)とわかります。電卓の使い方 おうぎ形の半径と中心角を入力して「計算」ボタンを押すと、おうぎ形の面積と弧の長さが計算されます。 円周率は変更できます。 円周率で「πを使う」にチェックを入れると円周率をπとして計算します。 半径を求めたい場合は、中心角
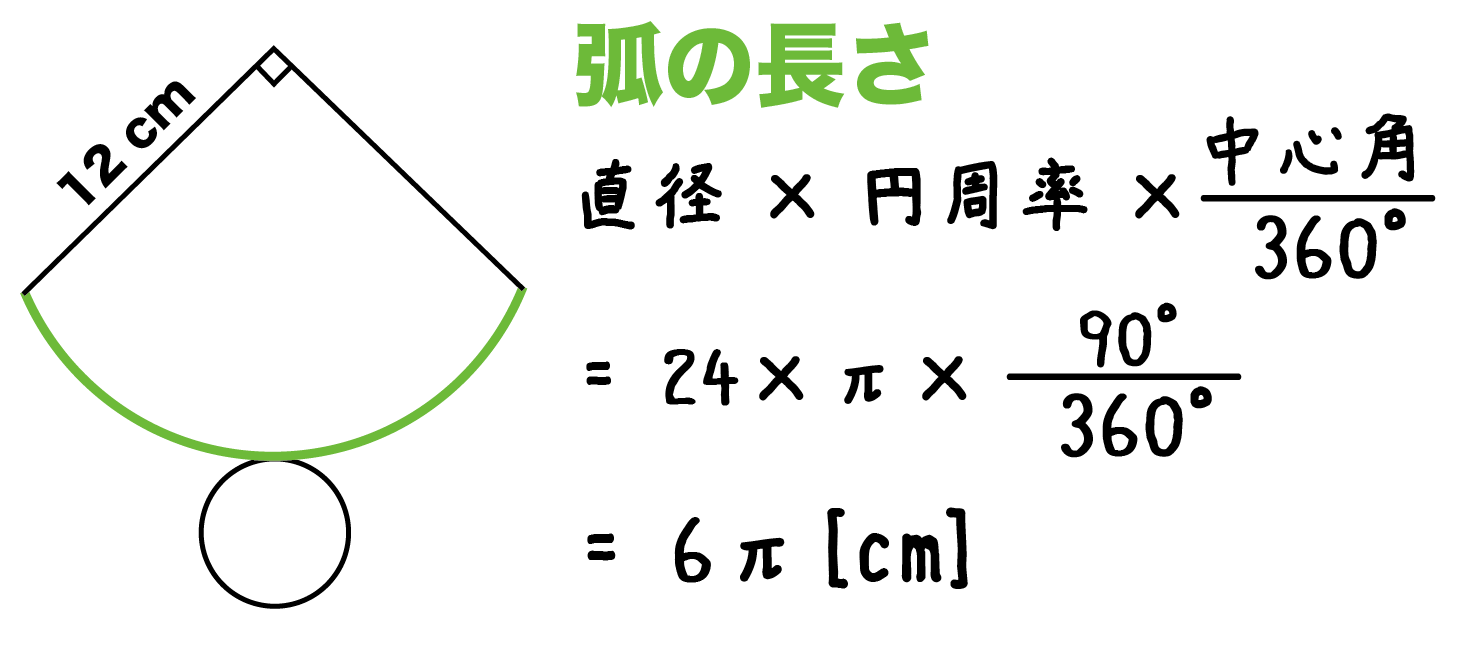
扇形の面積と弧の長さの求め方 扇形の面積 S × a ∘ 360 ∘ 例1) 中心角が 90 ∘ で、弧の長さが 628 c m の扇形の一辺の長さを求めなさい。 分からない部分を x として計算式にあてはめて計算します。 扇形の一辺の長さ x は直径の半分の長さですから おうぎ形の弧の長さ、面積、中心角の求め方と公式 19 February 16 おうぎ形は円を切りとったものです。 半分だけ切りとれば中心角は 1 8 0 ∘ 180^\circ 180∘ 、さらに半分切りとれば中心角は 9 0 ∘ 90^\circ 90∘ になります。 ケーキを半分に切ったり、三分 扇形の中心角をx°、弧の長さをL、半径をrとすると、x = 180L/πrになるってやつさ。 つまり、扇形の「半径」と「弧の長さ」がわかれば「中心角」を求めることができるんだ。たとえば、半径 4 、弧の長さが 6π の扇形があったとしよう。




扇形の弧の長さの求め方 公式と計算例




技術の森 弧の長さについて
イメージしにくいケースでは、以下のよう実際に図形を描いてみてもいいでしょう。 すると、2×3×314÷2 3×2 = 942 6 =1542 cmが答えとなるのです。 なお元の長さの単位がcm(センチメートル)であるため、同様に周の長さの単位もcmとなります。 さらに、もう一台例題を解いていってみましょう。 例題2 半径5cmの半円の周の長さを求めていきましょう工夫した解き方 特殊な問題を除くと、 円周や弧の長さ、円の面積やおうぎ形の面積は 「円周率の倍数 」です。 円周率が314のこの問題では、 弧の長さ157cmを「5×314」の形に変えておくことができます。 はじめにありました「覚えておきたい」で、 これは図形の見方が問われています回転とは何だろう? 回転移動して出来た下の図形は半径6cm, 中心角30°の扇形です また上の図形は元の図形と一致するので直径6cmの半円です さて色を塗った部分のまわりの長さは直径6cmの半円2つ分, つまり直径6cmの円周に相当します




扇形の公式は暗記しない 割合という考え方を導入するだけでスラスラ解ける 中学受験ナビ




扇形面積求め方 扇形の弧の長さと面積 小學 中學數學での平面図形の Txfs Co
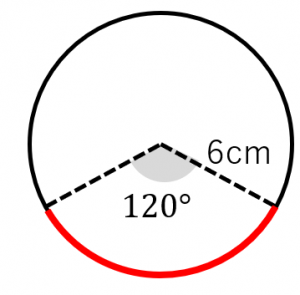
面積 大きい扇形−小さい扇形なので、 大 π×8×8×45/360=8π 小 π×4×4×45/360=2π 8π–2π=6π 周りの長さ 直線部分と曲線部分を2つずつ足したもの 直線部分は 44=8 →1 曲線部分は 小さい扇形、大きい扇形の弧の長さ。 小 2×π×4×45/360=π →2 大 2×π×8×45/360=2π →3 1〜3を全て足し 円周=直径×314 で求めることができますが 円周の長さを出すために、まず円の直径を知る必要があります。 この円の面積が096㎠であることから 円の面積=半径×半径×314=096(㎠) 半径×半径=096÷314= 64 同じ数をかけて64になるのは8。 半径が8cmとわかったので、直径はその2倍の16cm。 よって円周の長さは次のようになります。 この扇形の影のついた部分の周の長さを求めろという問題について質問です。 僕は、全体の弧の長さ影のついていない部分の弧の長さ+半径×2 だと思って、 2π×6×3分の12π×3×3分の1+6 =(2π+6)cm だと思ったのですが、回答が(6π+6)cmでした。
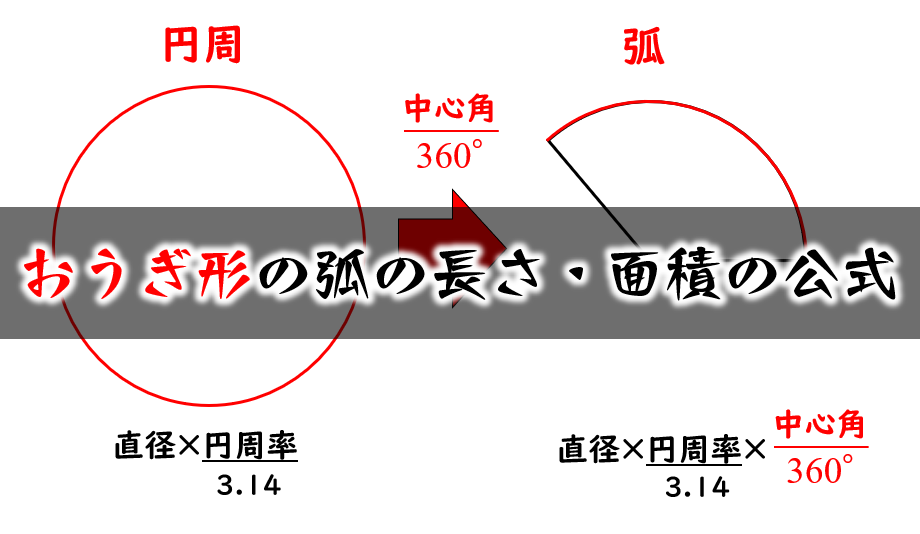



おうぎ形の弧の長さと面積の求め方 小学生に教えるための解説 数学fun
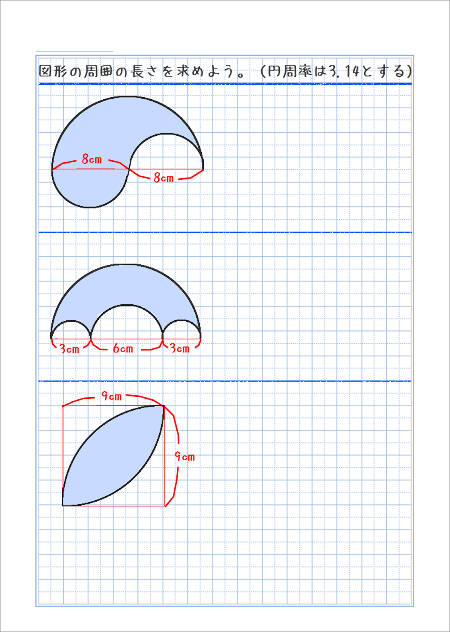



円周の長さの問題をもっと解いてみよう 家庭学習レシピ
About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators公式が覚えられない を解消 円とおうぎ形の周りの長さ 面積の求め方 中学受験ナビ 扇形の中心角を求める公式は、 x = 180 × 弧の長さ π × 半径 x = 180 × 弧 の 長 さ π × 半 径 弧の長さ= L、半径= r とすると、 x = 180L πr x = 180 L π r だよ 公式は忘れちゃったら解けないし、これを覚えるのは大変だ 円周の求め方と円の面積について アタリマエ 円を2つ合わせた面積を求める 色のついた部分の面積を求めます。 大きい円の面積から小さい円の面積をひきます。別々に求めても構いませんが計算式を1つにした方が早く答えを求めることが出来ます。 8×8×3144×4×314 = 64 ×



中学数学 円錐の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
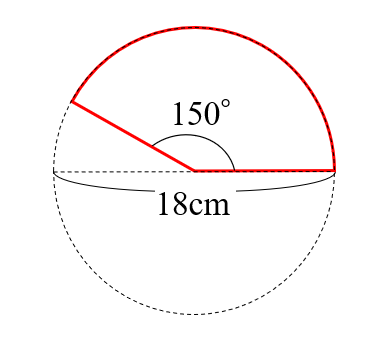
「扇形の弧の長さ」の求め方の基本はわかったね? ? それじゃあ、 扇形の弧の長さの公式 をみていこう! 扇形の半径をr、中心角をα、円周率をπとすると、 2πr×α/360 で「扇形の弧の長さ」を求められるんだ。 公式のうしろにある「 α/ 360 」という数値が「 扇形が円の 分の1になっている 」ってことをあらわしているよ。 つまり、「円」という1枚のピザを何等分に切ったか? ? と 長方形の面積の求め方を覚えている人は多くいます。 しかし、「なぜ縦×横になるのか」というのを理解していないこともあります。 面積と周りの長さを間違えるということが珍しくないですが、 その原因が公式の丸暗記です 。 本来は、 面積と周りの直径 18 18 cm、中心角 150° 150 ° のおうぎ形の周りの長さを求めよ。 おうぎ形は弧と2つの半径に囲まれているので、弧の長さと半径×2が周りの長さになります。 弧の長さ:18×314× 150 360 150 360 =18×314× 5 12 5 12 =157×15=2355 ( cm c m) 半径×2:18 ( cm c m) 周りの長さ:=4155 ( cm c m) 問題3 半径6cmのおうぎ形の弧の長さが314cmだった。 この扇形の



小5 算数 小5 55 円のまわりの長さ Youtube




2分でわかる 扇形 おうぎ形 の弧の長さの求め方 Qikeru 学びを楽しくわかりやすく
まずは、求めたい半径の大きさを\(x\)㎝とします。 すると、半径\(x\)㎝で中心角1°の扇形の弧の長さは $$2\pi \times x \times \frac{1}{360}=\frac{2}{3}\pi x$$ と表すことができます。 そして、弧の長さが\(6\pi\)㎝になるはずだから $$\frac{2}{3}\pi x=6\pi$$円弧の長さが2πのとき、半径の長さを求めます。 L=αr でした。αは、弧度法で表します。 α=50/180×π=028π L=2π 2π=028πr r=2π÷028π=714 です。 まとめ 今回は半径の求め方について説明しました。半径の求め方は、円の性質に関係します。円の周りの長さを計算しよう 家庭学習レシピ 扇形の弧の長さや面積を求めることには慣れている人でも え、半径!? どうやって求めるの? と、なってしまうことが多いです。 いざというときに困ってしまわないよう、半径を求める練習をしておきましょう。 スポンサーリンク Content




円 扇形 の面積 周や弧の長さの公式 数学fun




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット
影の部分の面積、周の長さ(2)の解説 面積を求めるには、大きなおうぎ形から小さなおうぎ形を引けばよいですね。 周の長さを求めるには、 小さなおうぎ形の弧(赤)、大きなおうぎ形の弧(青) そして、それぞれの半径の差の部分(緑)に分けることができます。 それぞれを計算して、合計すると次のようになります。扇(おうぎ)形の面積を求める公式3つと弧の長さの求め方をお伝えします。 面積と弧の長さは比例ですべて解けるのですがこれを苦手にしている中学生はものすごく多いです。 これには当然とも言える理由が3つあります。 ここで図形を算数 大舘 国士 「難しい問題の解き方」の解説! 円とおうぎ形の周りの長さ、面積を求める応用問題3選! 今回は平面図形の入試問題の中から,とりわけ 難易度の高い応用問題を3問 ご紹介いたします。 このような応用問題は基礎を身につけた上




扇形の弧の長さの求め方 たぬぬ塾 中学校の先生たち




扇 おうぎ 形の面積を求める公式と弧の長さの求め方
扇形とは 面積 中心角 半径 弧の長さの公式と求め方 受験辞典 数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo 公式を図解 すい体の体積 円すいの表面積 の公式




公式を図解 すい体の体積 円すいの表面積 の公式の求め方と使い方 中学受験ナビ




扇形の中心角の求め方 途中式をていねいに解説 面積 弧の長さから求める方法 中学数学 理科の学習まとめサイト
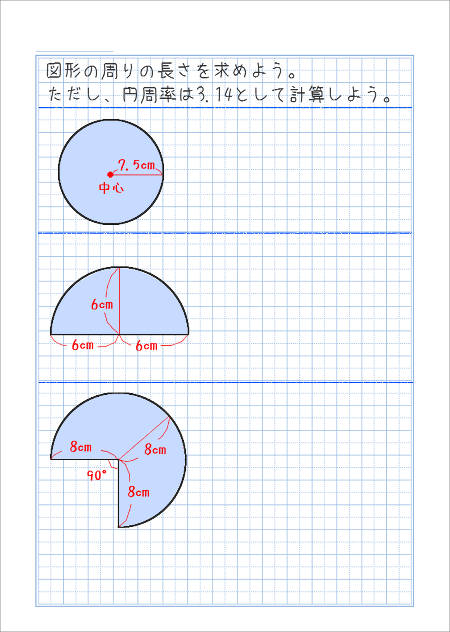



円の周りの長さを計算しよう 家庭学習レシピ




図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト



扇形の弧の長さは 1分でわかる求め方 公式 面積 ラジアンとの関係




扇の弧の長さと面積の求め方 公式 中学数学 By Okボーイ マナペディア




扇形の弧の長さと面積 小学 中学数学での平面図形の求め方 Hatsudy 数学 科学




扇形の面積 弧の長さ まわりの長さの求め方 公式 小学生 中学生の勉強




難しい問題の解き方 の解説 円とおうぎ形の周りの長さ 面積を求める応用問題3選 中学受験ナビ




2分でわかる 扇形 おうぎ形 の弧の長さの求め方 Qikeru 学びを楽しくわかりやすく
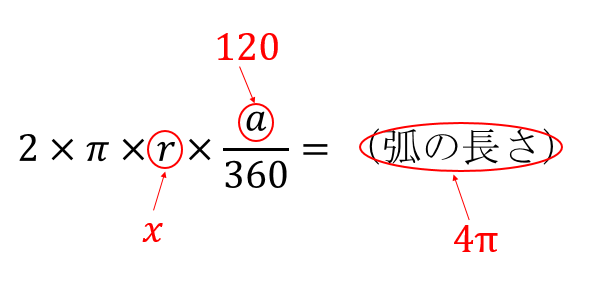



おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ




Circle2 小学校算数 おうぎ形の弧の長さ Youtube




おうぎ形の弧長 面積 中心角 半径 具体例で学ぶ数学
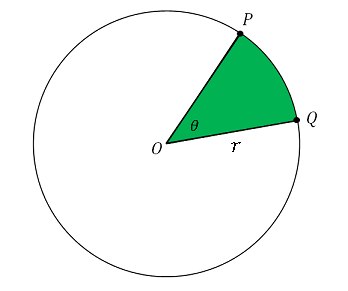



扇形の弧の長さと面積 Excel Vba 数学教室



1




円錐の側面積 展開図の扇形の中心角 扇形の面積の求め方について 身勝手な主張




扇形面積の求め方 扇形の面積公式が一目でわかる 丁寧な証明付き 高校 Qkaxtw




扇形の中心角とは 求め方って 円周や面積や弧の長さを使って計算 ノビコト
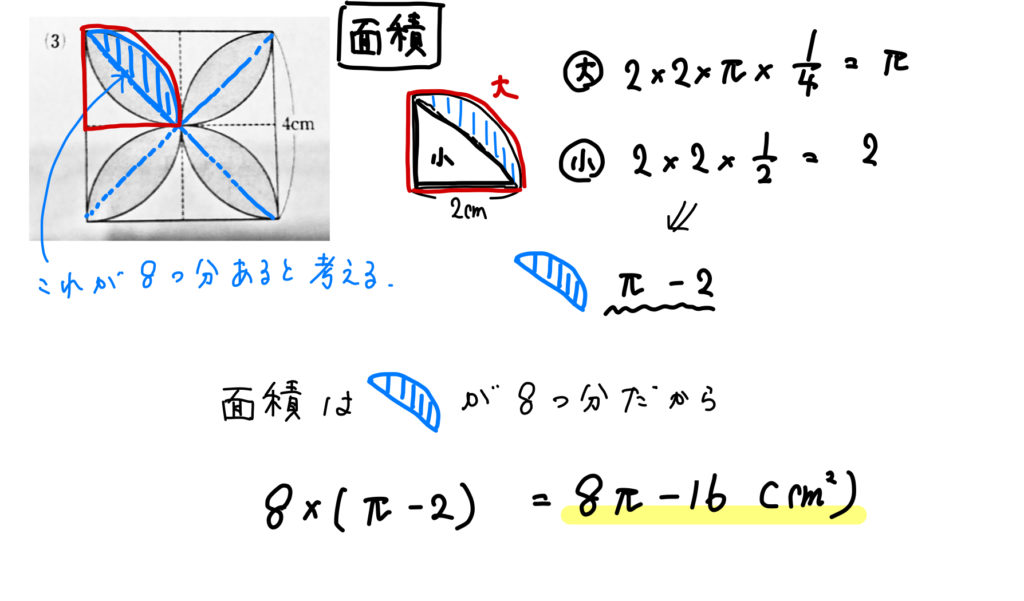



おうぎ形の応用 影の部分の面積 周の長さの求め方 数スタ




扇形 周の長さの求め方をイチから解説するぞ 中学数学 理科の学習まとめサイト




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット




扇形の弧の長さと面積 小学 中学数学での平面図形の求め方 Hatsudy 数学 科学




2分でわかる 扇形 おうぎ形 の弧の長さの求め方 Qikeru 学びを楽しくわかりやすく



扇形とは 面積 弧の長さ 中心角 半径の公式と求め方 受験辞典




2分でわかる 扇形 おうぎ形 の弧の長さの求め方 Qikeru 学びを楽しくわかりやすく




中1 数学 中1 75 おうぎ形の弧と面積 基本編 Youtube



1




扇形の面積の出し方と特殊な場合の公式 たぬぬ塾 中学校の先生たち




扇形の面積の求め方 公式と計算例
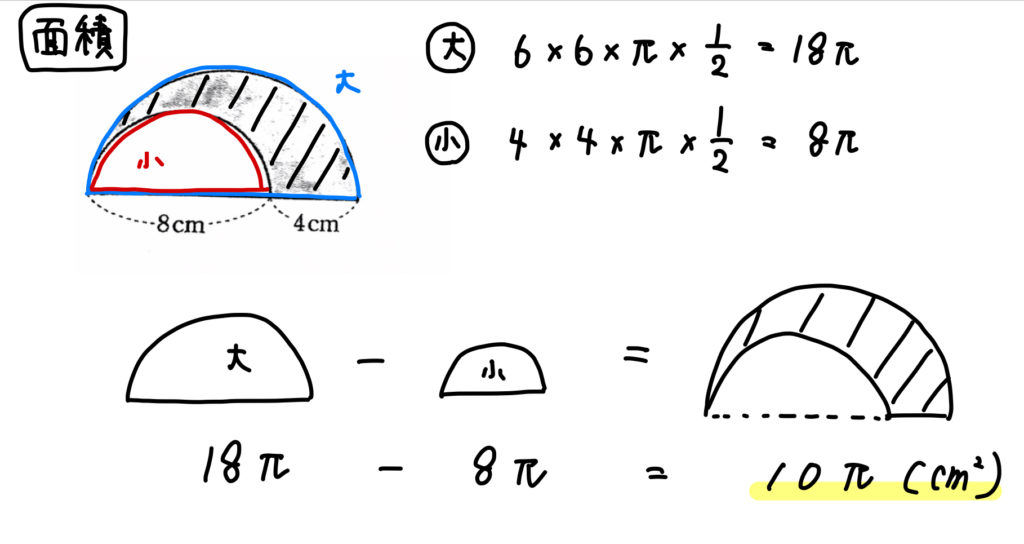



おうぎ形の応用 影の部分の面積 周の長さの求め方 数スタ




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




扇形面積の求め方 扇形の面積公式が一目でわかる 丁寧な証明付き 高校 Qkaxtw




周りの長さ おうぎ形 Youtube




扇形の面積の求め方 小学生でも公式を簡単に使える問題です 中学や高校の数学の計算問題




中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット




3分で分かる 扇形 おうぎ形 の面積と弧の長さの求め方 公式をわかりやすく 合格サプリ




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者
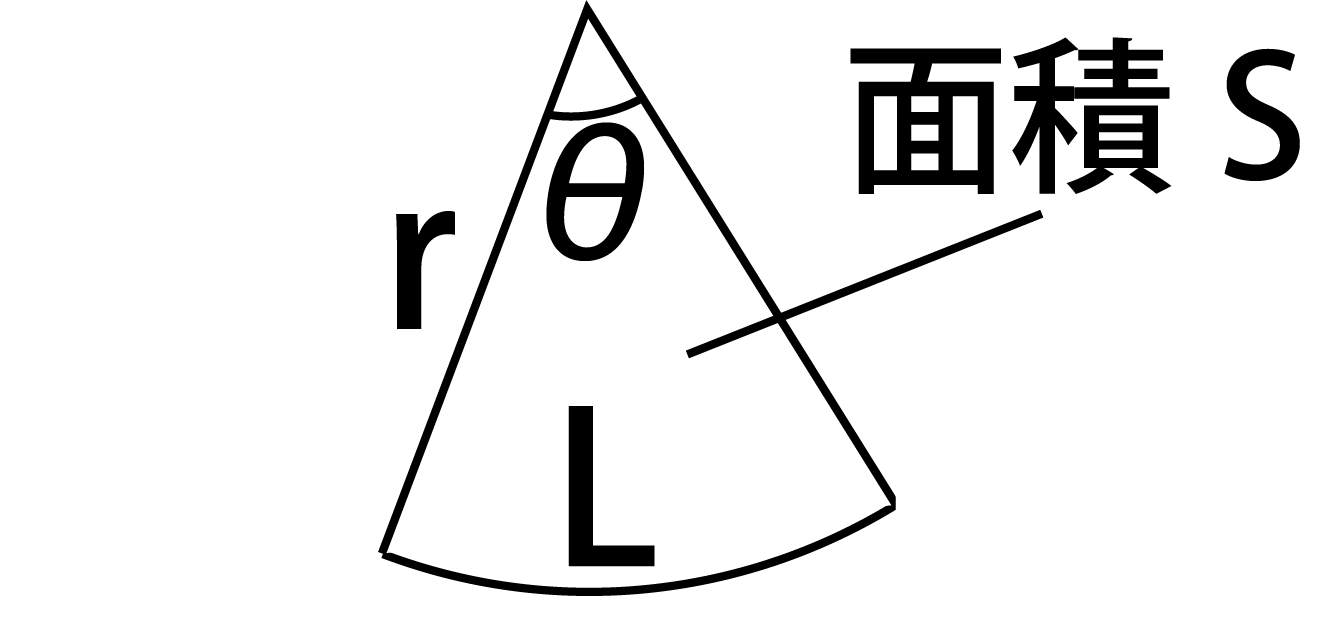



扇形の面積公式が一目でわかる 丁寧な証明付き 高校生向け受験応援メディア 受験のミカタ




中1 数学 中1 77 おうぎ形の弧と面積 ややこしい図形編 Youtube



扇形とは 面積 弧の長さ 中心角 半径の公式と求め方 受験辞典




おうぎ形の弧の長さと面積の求め方 小学生に教えるための解説 数学fun




円の周りの長さを計算しよう 家庭学習レシピ



1




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



扇形とは 面積 弧の長さ 中心角 半径の公式と求め方 受験辞典
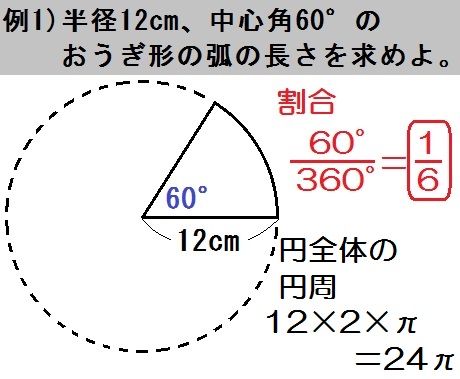



中学数学 平面図形 のコツ 円とおうぎ形




扇形面積公式弧長 3分で分かる 扇形 おうぎ形 の面積と弧の長さの Mtlpe




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ
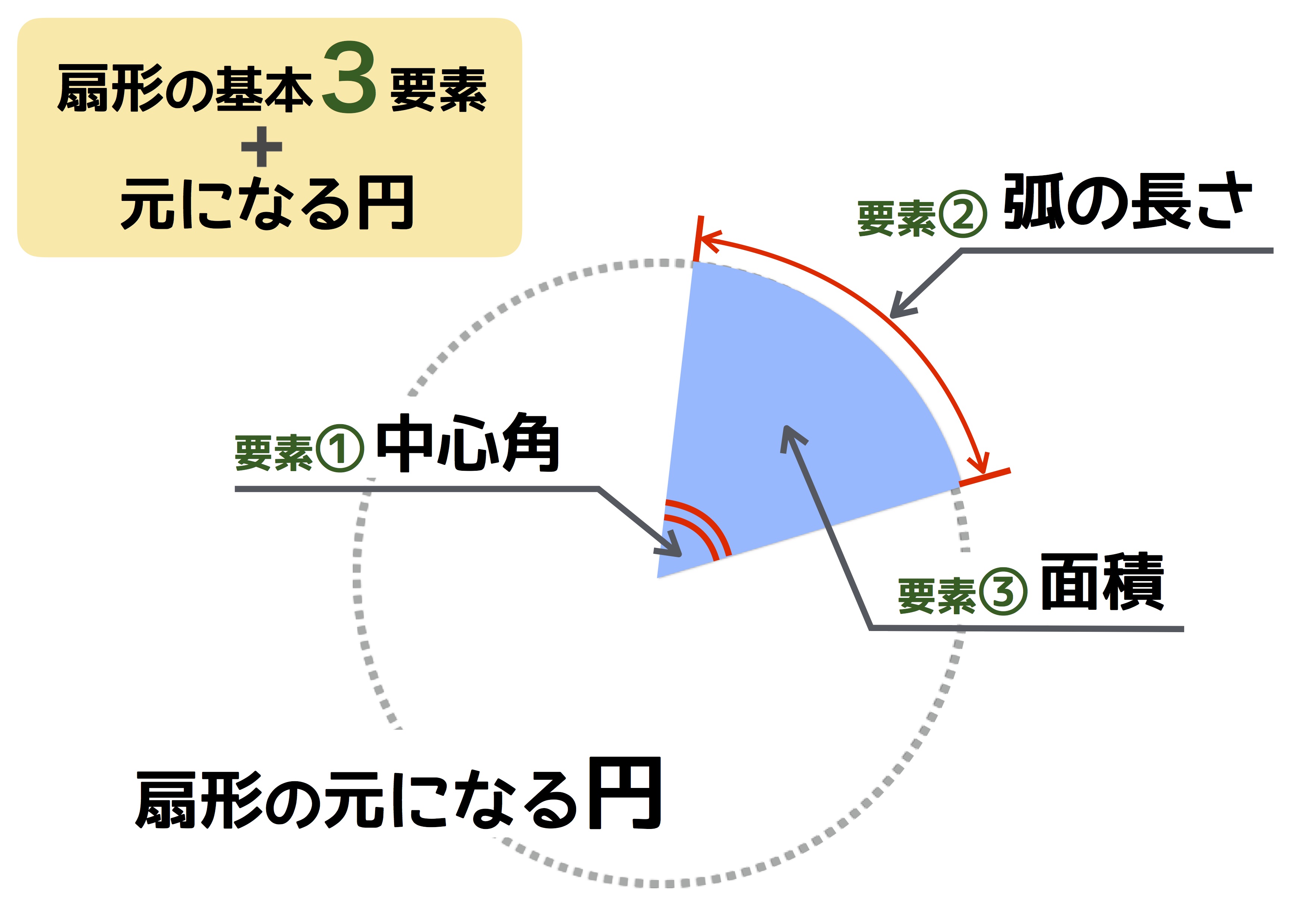



扇形の公式は暗記しない 割合という考え方を導入するだけでスラスラ解ける 中学受験ナビ




円 扇形 の面積 周や弧の長さの公式 数学fun



扇形の弧の長さと面積 数学ii フリー教材開発コミュニティ Ftext




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者




扇形の面積公式が一目でわかる 丁寧な証明付き 高校生向け受験応援メディア 受験のミカタ



弧の長さと弦の長さの求め方 円周角との関係など 具体例で学ぶ数学



扇形とは 面積 弧の長さ 中心角 半径の公式と求め方 受験辞典



おうぎ形 注意 周りの長さを求める公式を解説 数スタ



おうぎ形の応用 影の部分の面積 周の長さの求め方 数スタ




小学5年生の算数 円 おうぎ形 問題プリント ちびむすドリル 小学生




円 半円 弧 扇形 の円周 面積の求め方と公式一覧 小学生の算数 Yattoke 小 中学生の学習サイト
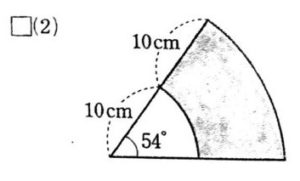



おうぎ形の応用 影の部分の面積 周の長さの求め方 数スタ
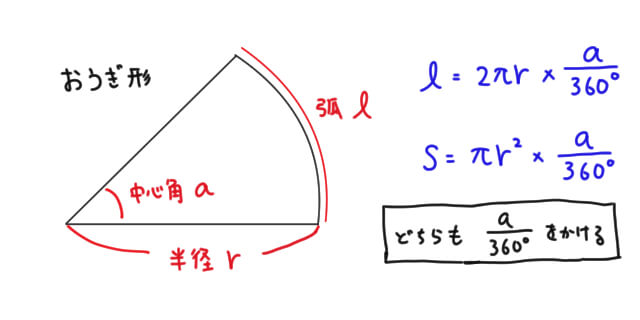



おうぎ形の弧の長さ 面積 中心角の求め方と公式 Irohabook



1




扇形 周の長さの求め方をイチから解説するぞ 中学数学 理科の学習まとめサイト




公式が覚えられない を解消 円とおうぎ形の周りの長さ 面積の求め方 中学受験ナビ
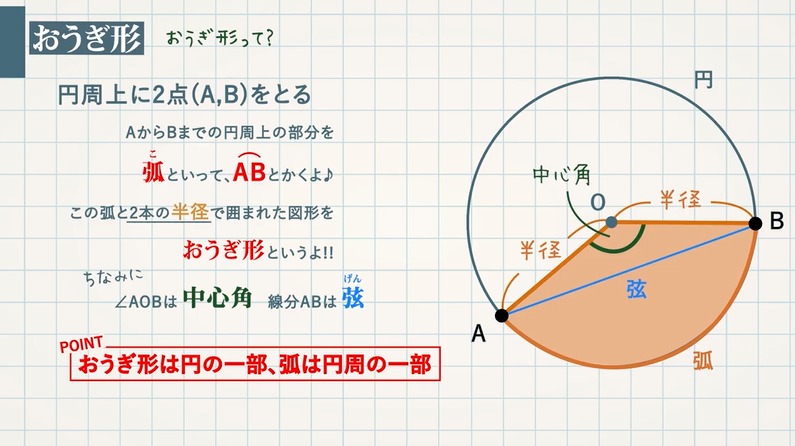



おうぎ形まとめ 弧と面積の求め方 教遊者




おうぎ形 注意 周りの長さを求める公式を解説 数スタ




おうぎ形の問題 ちょっと応用編 切り取って求める 苦手な数学を簡単に




円 扇形 の面積 周や弧の長さの公式 数学fun
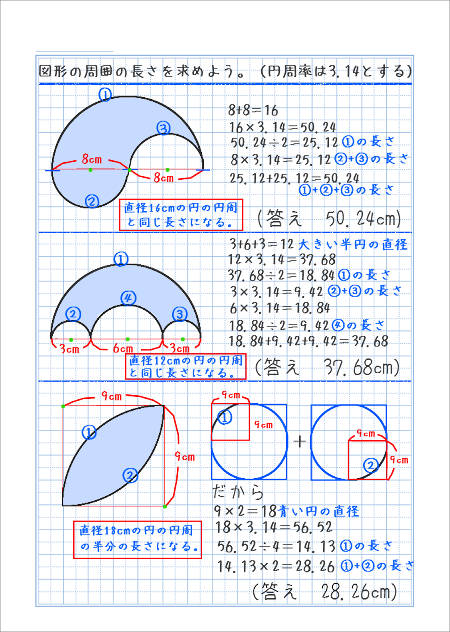



円周の長さの問題をもっと解いてみよう 家庭学習レシピ




平面図形 おうぎ形の中心角の求め方 中学数学 定期テスト対策サイト



弧の長さと弦の長さの求め方 円周角との関係など 具体例で学ぶ数学




円周の求め方 公式は直径を使うので 半径と間違えないように 中学や高校の数学の計算問題




扇形面積の求め方 扇形の面積公式が一目でわかる 丁寧な証明付き 高校 Qkaxtw




扇形の弧の長さの求め方 公式と計算例



おうぎ形の弧の長さと面積の求め方 小学生に教えるための解説 数学fun



数 三角関数 円弧の長さと扇形の面積 オンライン無料塾 ターンナップ Youtube



扇形とは 面積 弧の長さ 中心角 半径の公式と求め方 受験辞典




扇形の弧の長さの公式 簡単な問題で求め方をマスターしよう 中学や高校の数学の計算問題




3分で分かる 中心角の求め方ー公式とその証明 練習問題をわかりやすく 合格サプリ



弧の長さと弦の長さの求め方 円周角との関係など 具体例で学ぶ数学
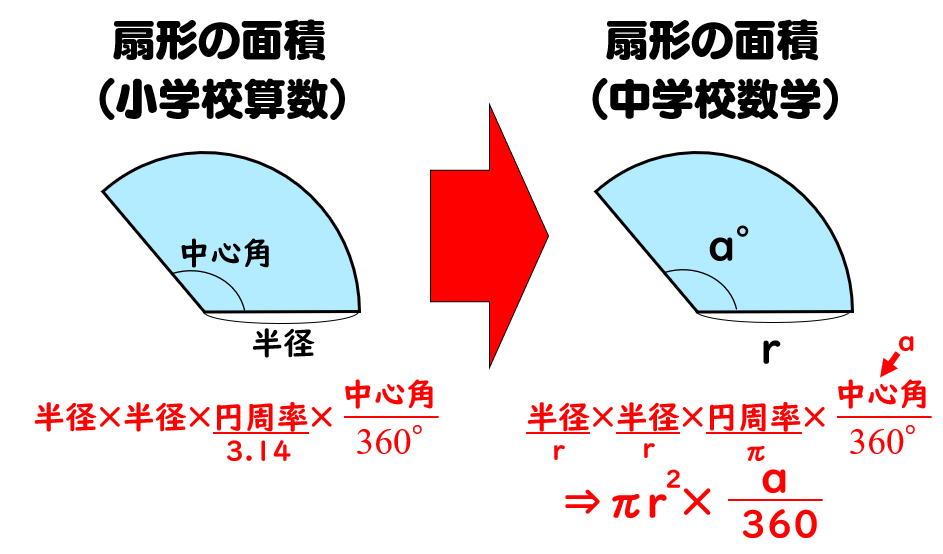



円 扇形 の面積 周や弧の長さの公式 数学fun




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット




扇形 周の長さの求め方をイチから解説するぞ 中学数学 理科の学習まとめサイト



3分で分かる 扇形 おうぎ形 の面積と弧の長さの求め方 公式をわかりやすく 合格サプリ




公式が覚えられない を解消 円とおうぎ形の周りの長さ 面積の求め方 中学受験ナビ




公式が覚えられない を解消 円とおうぎ形の周りの長さ 面積の求め方 中学受験ナビ




扇形の弧の長さの公式 簡単な問題で求め方をマスターしよう 中学や高校の数学の計算問題




扇形の面積 弧の長さ まわりの長さの求め方 公式 小学生 中学生の勉強
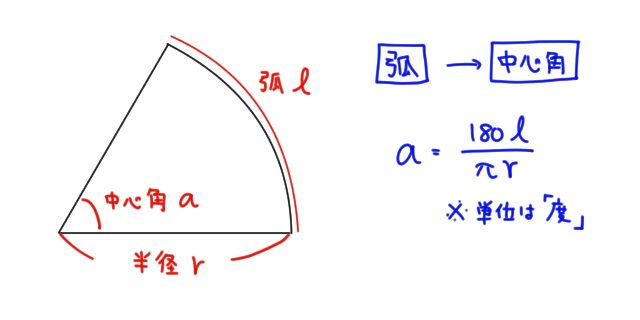



おうぎ形の弧の長さ 面積 中心角の求め方と公式 Irohabook



0 件のコメント:
コメントを投稿